A que distância você consegue ver um meteoro?
>Eu recebo e-mail.
A maioria está fazendo perguntas de vários tipos, a maioria das quais bastante simples de responder (na verdade, muitas podem ser respondidas pesquisando no Google, dica dica). Mas às vezes eu recebo uma pergunta que é mais difícil de responder, ou mesmo uma que já me perguntei sobre mim, mas nunca tive tempo de descobrir.
Fiquei muito intrigado quando recebi uma pergunta do Bad Reader Dean Lewis sobre meteoros. Durante a chuva de meteoros Perseidas em 2018, ele estava longe de sua família, separado por cerca de 1.000 quilômetros. Se ele visse um meteoro, seria possível que eles pudessem ver o mesmo de seu local mais distante?
A resposta curta é sim! A longa resposta é ... matemática. Matemática legal e divertida.
E vendo como, quando este artigo for postado, a chuva de meteoros Geminid anual de 2018 atinge o pico esta noite, acho que é apropriado descobrir isso.
Crash Course Astronomy: Meteors, Meteoroids, and Meteorites, Oh My!
Se a Terra fosse perfeitamente plana, então, em princípio, você poderia ver um meteoro até qualquer borda da Terra. Enquanto você estiver acima do solo, mesmo um pouquinho, sua linha de visão atinge cada centímetro quadrado do planeta ao seu lado, de modo que cada meteoro é visível para todos. Na realidade, o ar não é perfeitamente transparente, então a certa distância você está olhando através de tanta sujeira que não consegue ver nada.
No entanto, a Terra não é plana. A sério! É redondo. E a atmosfera o envolve como uma concha, ficando mais tênue com a altura e eventualmente desaparecendo; essa altura depende da sua definição de espaço. No entanto, podemos trapacear um pouco, já que conhecemos ciência: meteoros como aqueles em chuvas tendem a queimar cerca de 100 quilômetros acima do solo. Essa altura depende de muitas coisas, incluindo o tamanho do meteoróides (os pedaços sólidos de destroços interplanetários zunindo pelo espaço), quão rápido eles estão se movendo, em que ângulo eles entram na atmosfera, e assim por diante. Mas vamos chamá-lo de 100 km.
O mais próximo que um meteoro pode estar de você é se você estiver diretamente sob ele, e então ele está 100 km em linha reta (no seu zênite). Se ele queimar mais longe do zênite, deve estar mais longe de você. O mais distante que você pode ver um meteoro, é lógico, é, portanto, se ele estiver exatamente no horizonte.
A geometria se parece com isto (nota: NÃO está em escala):
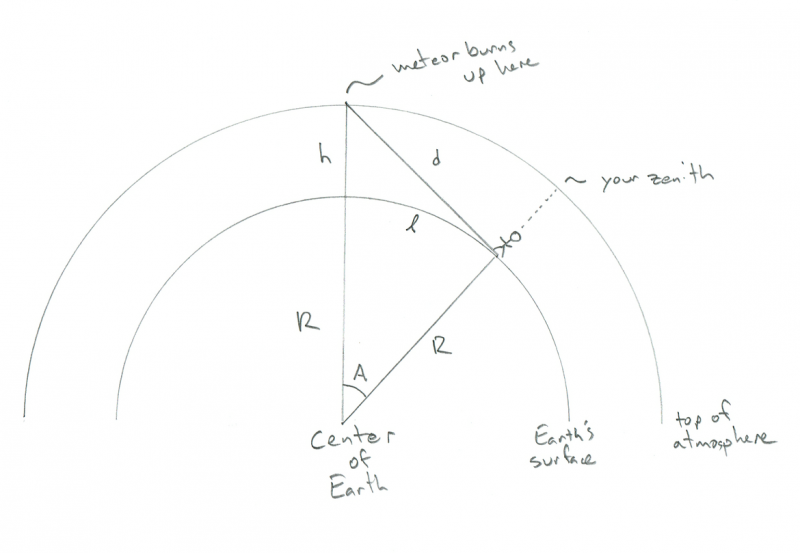
Esquema mostrando a geometria de um observador assistindo a queima de um meteoro. Crédito: Phil Plait
Você pode ver a pequena figura humana em pé na superfície da Terra curva - digamos que seja você - com a atmosfera (também curva) acima deles. Neste diagrama, R é o raio da Terra (6.400 km), h é a altura que o meteoro queima (100 km) e d é a distância de você até o meteoro. A é o ângulo entre a sua posição na Terra e a posição do meteoro acima dela, e a cursiva l (como em comprimento) é a distância que você teria que caminhar para que o meteoro estivesse diretamente acima (eu sei que parece uma coisa estranha querer saber, mas tenha paciência comigo). Estranhamente, você pode calcular tudo o que precisa aqui sem saber d, mas vamos lá, é legal saber a que distância está o meteoro, certo?
mune el guardián de la luna
A chave para tudo isso é ver que o ângulo entre o meteoro, você e o centro da Terra é um ângulo reto. Isso ocorre porque o meteoro está no horizonte conforme visto por você (ou, se você preferir um jargão divertido, na linha tangente no círculo interno onde R o cruza). Isso torna o triângulo um triângulo retângulo, e se você se lembra da matemática do ensino médio, isso significa que pode encontrar todos os lados e ângulos!
Lembrar o teorema de Pitágoras ? Em um triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos outros dois lados*. Em nosso triângulo, a hipotenusa é R + h, e os outros lados são R e d.
Então
(R + h)2= d2+ R2
ou, multiplicando o lado esquerdo (use FRUSTRAR ):
R2+ 2Rh + h2 = d2+ R2
Resolva d para ver a que distância o meteoro está de você. Observe que R2 está em ambos os lados, então cancele-os para obter
la carta estelar invertida
d2= 2Rh + h2
Ou
d = raiz quadrada (2Rh + h2)
Bem, nós sabemos todos esses números! Plug-n-chug, baby:
d = raiz quadrada (2 x 6.400 x 100 + 10.000) = 1.136 km
Aha! Isso significa que se você vir um meteoro no horizonte, ele está a mais de 1.100 quilômetros de distância! É um longo caminho e, tecnicamente, o mais distante que você pode ver um meteoro do solo.
Agora vamos encontrar a letra l. Primeiro, precisamos saber o ângulo A. Isso requer alguma trigonometria. Há muitos identidades trigonométricas você pode usar para descobrir isso, mas meu favorito†é que, em um triângulo retângulo, o seno de um ângulo é o comprimento do lado oposto dividido pelo comprimento da hipotenusa. Então, se conseguirmos essa razão, podemos pegar o seno inverso (ou arco seno) para obter o ângulo.
sen (A) = d / (R + h)
assim
A = sem-1(d / R + h)
Plug-n-chug novamente e obtenho A = 10 °. Esse é um pedaço decente da superfície da Terra!
E agora podemos usar o cursivo l. Existem 360 ° ao redor da Terra, e a circunferência da Terra é 2 x pi x raio = 40.192 km, então há
40.192 km / 360 ° = 112 quilômetros por grau
o que significa, por sua vez, 10 ° = 1.120 quilômetros. Isso é muito próximo de d, o que não é muito surpreendente. Os desenhos são exagerados, mas na realidade a concha de ar sobre nós é pequena se comparada ao tamanho da Terra. Se eu fizesse os desenhos em escala, você veria que d e l realmente são muito próximos em comprimento.
OK, então por que estou com tanto calor e me incomodando em encontrá-lo? Por causa da pergunta original! Se você esqueceu depois de toda aquela matemática, é quão longe duas pessoas podem estar e ainda ver o mesmo meteoro?
Bem, nesse caso o meteoro estaria diretamente entre eles, e em cada um de seus respectivos horizontes. Essa geometria se parece com isto:
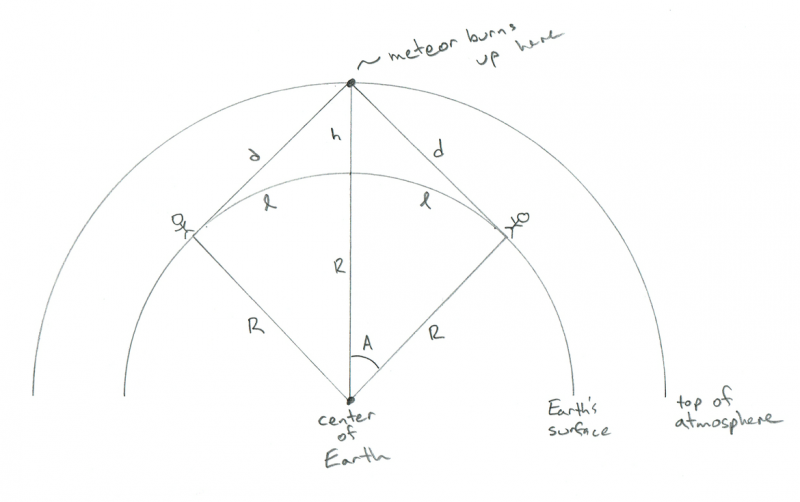
Esquema mostrando a geometria de dois observadores assistindo a um meteoro queimando exatamente entre eles. Crédito: Phil Plait
Significado del número 331
AHA! Agora você vê porque eu quero! A distância entre as duas pessoas é de apenas 2 x l! Portanto, agora temos a resposta:
Para que duas pessoas vejam o mesmo meteoro, eles não podem estar separados por mais de 2 x 1.120 = 2.240 quilômetros. Por exemplo, é muito perto da distância entre Washington, DC e Denver. Uau.
A propósito, para uma mudança de perspectiva (literalmente), isso significa que do ponto de vista do meteoro, ele pode ver um trecho da Terra com 2.240 quilômetros de largura (como em, DC na parte oriental da Terra e Denver na parte ocidental). Isso é bem legal.
E isso nos leva à resposta real à pergunta de Dean: se ele estava a 1.000 km de sua família, então sim, tecnicamente eles poderiam ver o mesmo meteoro. Que tal isso?
Agora, isso novamente assume que o ar está perfeitamente limpo e tudo mais, o que na realidade é essencialmente impossível. Portanto, esta matemática representa uma situação ideal (incluindo a ideia de que o meteoro está exatamente entre eles).
Vamos ser mais realistas. Digamos que o meteoro queime no céu a uma altitude de 45 ° acima do horizonte para ambos os observadores. A que distância eles estariam um do outro? Bem, novamente assumindo que o meteoro está exatamente entre eles, a geometria é mais assim:
la vida secreta de walter mitty revisión
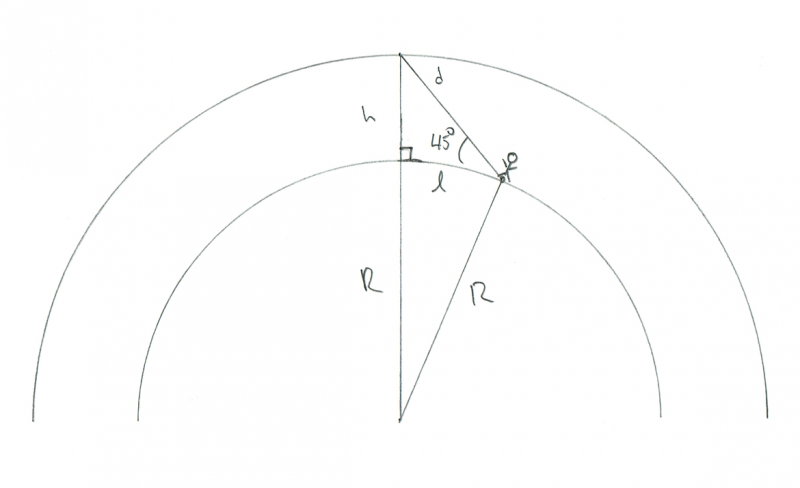
Esquema mostrando a geometria de um observador observando um meteoro queimando 45 ° acima do horizonte. Crédito: Phil Plait
Na verdade, isso é mais difícil de resolver, mas conheço outro truque: se presumirmos que sou pequeno, a curvatura da Terra não será importante. Por exemplo, se eu quiser saber a distância entre duas árvores em meu quintal, não me importo se a Terra é curva. Em uma distância tão pequena, posso assumir que é plano. Vamos fazer essa suposição aqui.
Nesse caso, temos outro triângulo retângulo, mas desta vez o ângulo reto é aquele sob o meteoro. Eu até o rotulei no diagrama com a notação quadrada pequena. Então, se esse é um ângulo de 90 °, e nosso ângulo com o meteoro é de 45 °, então o último ângulo (do meteoro para o observador) também é de 45 °. Isso significa que este deve ser um triângulo isósceles, então leh são iguais! Como sabemos que h é 100 km, l também deve ser.
E isso significa que a distância entre nossos dois observadores é o dobro disso, ou 200 km.
Aliás, neste caso, a distância até o meteoro é de cerca de 141 km. Vou deixar isso como um exercício para o leitor.
Em princípio, isso significa que, se você souber a que distância do horizonte está um meteoro e a altitude em que ele se incendiou, poderá calcular sua distância (ou se souber a distância, poderá obter sua altura). Essa trigonometria é muito complicada, porém, e acho que já joguei matemática suficiente para você por hoje.
Mas é legal pensar que um pouco de matemática do ensino médio pode ter uma aplicação tão divertida. E devo admitir que é poético e romântico saber que, desde que a separação não seja muito grande, é possível compartilhar a visão de uma estrela cadente com outra pessoa. Que pensamento adorável.
* Em O feiticeiro de Oz , o espantalho entendeu errado depois ele tem um cérebro.
† Do curso Eu tenho uma identidade trigonométrica favorita. O que é seu?













